50 éves a Black–Scholes-model, a modern pénzügyek sarokköve

Fischer Black és Myron Scholes közgazdászok „The Pricing of Options and Corporate Liabilities” című cikküket éppen ötven éve, 1973-ban publikálták – melynek nyomán később Robert C. Merton matematikus tette közzé tudományos folyóiratban a fent említett két közgazdász után csak „Black–Scholes options pricing model”-ként hivatkozott matematikai keretrendszert. Az igazsághoz hozzátartozik, hogy az opciók árazására már a 60-as években is léteztek több-kevesebb sikerrel a gyakorlatban is alkalmazott módszerek, ugyanakkor ezek még korántsem voltak tudományos alapossággal kidolgozva.

Fenti három kutató közül ketten, Merton és Scholes 1997-ben munkásságukért megkapták a Közgazdasági Nobel-emlékdíjat. Black 1995-ben bekövetkezett halála miatt (a díjat jelölt csak életében kaphatja meg) nem szerepelt a díjazottak között, de a Svéd Akadémia, őt is megemlítette közreműködőként.

Az egyenlet bekerült Ian Stewart matematikus 2013-ban publikált 17 egyenlet, ami megváltoztatta a világot című tudománynépszerűsítő könyvébe. A Black–Scholes ezzel egyenesen a relativitáselmélettel, a kvantum mechanikával, vagy éppen a Pitagorasz-tétellel került egy klubba.

A modell eredményeit a kvantitatív pénzügyek számos területén használják, előkerül a kockázati modellezésben, reálopciók árazásában és szinte mindenhol, ahol árazási helyzeteket valószínűségi változóként kezelünk.

Mi az az opció?

Az opció valamilyen alaptermékre (például részvényre) szóló, lejárattal rendelkező vételi (call) vagy eladási (put) jog, egy előre rögzített áron (strike price). Például tegyük fel, hogy az ABC részvény ára jelenleg 1000 forint. Mennyit érhet egy olyan eladás jog, amivel a következő egy évben 900 forinton eladhatjuk a részvényt? Mivel a részvény jelenleg a piacon drágábban is eladható, ez az opció jelenleg értéktelennek tűnhet (out of the money), de mivel az ABC részvénnyel bármi történhet a következő egy év során, így az eladási jog felfogható egyfajta biztosításként, hogy a részvényt akkor is eladhatjuk 900-on, ha esetleg a piacon ez alá az érték alá esne. Hogy a jelenben pontosan mennyit ér egy ilyen jog, többek között erre a problémára kínál megoldást a Black–Scholes-formula.

Egy opció ára két tényezőből áll össze: Ha az opció kötési ára az alaptermék aktuális piaci áránál kedvezőbb, akkor a két ár különbsége az opció ún. belső értéke (intrinsic value). A lejáratig tartó bizonytalanságból fakadó értéket pedig időértéknek (time value, vagy időnként extrinsic value) nevezzük. Fenti példában az opciónak csak időértéke van, de belső értéke nincs.
Az opcióárazás lényege a bizonytalanságért fizetendő prémium. Egy vételi, vagy eladási jog esetében a bizonytalanság leegyszerűsítve a részvényárfolyam változékonyságának (volatilitásának), valamint a hátralévő időnek valamilyen függvénye. (A kockázatmentes hozam szintjétől, az esetleges osztalékoktól és egyéb zavaró tényezőktől az egyszerűség kedvéért most tekintsünk el!)
A lejárat pillanatában pontosan tudjuk az opció értékét, hiszen az annyi, mint amennyivel az opció kötési ára (strike price) számunkra kedvezőbb az alaptermék aktuális piaci áránál. (Ha az ABC részvény most csak 800-at ér, de nekünk van egy 900-as kötési árra szóló eladási jogunk, akkor az a jog 100-at ér.) Ha a lejáratkor az opciónak nincs belső értéke, akkor nullát ér, hiszen ekkor már időértéket sem hordoz magában. Ugyanakkor a lejárat előtti időszakban még nem tudhatjuk, hogy az opció lejárata pillanatában az alaptermék ára éppen mennyi lesz, így erre vonatkozólag egy bizonyos mértékű szórásból és a hátralévő idő hosszából adódó válószínűséggel számolhatunk. Fenti példánál maradva, ha az ABC részvény jelenleg 1000 forint, akkor máshogy fog viselkedni egy 200-as, egy 500-as, vagy épp egy 1500-as eladási jog, mivel ezeknek más és más lesz a beválási valószínűsége (moneyness). Minél valószínűbb az adott kötési ár „beválása” lejáratkor (deep in-the-money), az opció árában annál kisebb a bizonytalanság (idő érték), tehát az opció maga már szinte hasonlít egy az alaptermékre kötött forward ügyletre. Ugyanez fordítva is igaz: ha az opció kötési ára nagyon valószínűtlenné teszi a lejáratkori lehívást, az opció nagyon olcsó lesz, hiszen valószínűleg belső érték nélkül fog lejárni. A pénzben történő lejárat bizonytalansága, azaz az időérték aránya az opció árában tehát az alaptermék aktuális árfolyama körüli strike price-okon (at-the-money) a legmagasabb.

Mit mond a modell

De nézzük meg ezt a problémakört kicsit mélyebb szakmai alapossággal! A Black–Scholes-modell feltételezi, hogy létezik legalább egy kockázatos termék, aminek árfolyama sztochasztikus, Brown-mozgást végez állandó volatilitás és drift (a szochasztikus változó várható értékének átlagos változása) mellett. Emellett létezik egy kockázatmentes eszköz (kamatláb), aminek hozama konstans, valamint fennállnak az általános CAPM modell feltételezései (nincs arbitrázslehetőség, azonos feltételei vannak a hitelnek és a betétnek, valamint a long és short pozícióknak és nincsenek tranzakciós költségek).
A Black–Scholes fenti előfeltételek megléte esetén az arbitrázsmentesség elvével bizonyítja, hogy egy opciónak egyedi ára van, ezzel gyakorlatilag elválasztva a derivatíva árát a mögöttes terméktől. Teszi ezt úgy, hogy az opciót szintetikusan replikálja egy modellportfólióval, aminek az értéke a fenti eszközökből előállítva egyértelműen meghatározható. Ha a szintetikus termék beárazható, akkor az opció árát is ismerjük, hiszen egy arbitrázsmentes piacon a kettőnek meg kell egyeznie.
Fentiekből alakult ki a folyamatos delta-fedezés konstrukciója, amelyet a mai napig használnak derivatív pozíciók árfolyamkockázatának eliminálására.

Mit mond a matek

A Black–Scholes-modelből következő ún. Black–Scholes-egyenlet az alábbi (európai call-ra vonatkozóan):

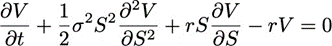
Ez egy parciális differenciálegyenlet, ami leírja az opció árát befolyásoló hatások összefüggéseit, ahol V az opció értéke S alaptermék és t idő függvényében, r kamatláb esetén. A szigma (σ) az alaptermék loghozamainak szórása, ami viszont érdekessé teszi ezt az egészet, hogy a valódi opciós piacon a szórás előretekintő, tehát nem olvasható le a múltbéli adatokból.

Ez a jelenség vezeti be az ún. implicit volatilitás fogalmát, ami azt jelenti, hogy az egyes szereplők által kialakított opciós árakból számolják vissza, hogy adott árazás mekkora szórást vetít előre, azaz az opciókereskedők adott időszakra (lejáratra) mekkora kockázatot látnak az alaptermék árfolyamában. Ezáltal az opció ára a többi paraméter ismeretében gyakorlatilag kifejezhető a várható szórásban, ami egyúttal megnyitja az utat a volatilitás önálló pénzügyi termékként történő kereskedése előtt.

Vizuálisan talán könnyebb megérteni a fentieket az alábbi ábra alapján. A lenti képen az látható, hogy a Google részvényre szóló opciók árai egy ún. volatilitási felületet alkotnak a lejáratig hátra lévő idő, valamint a kötési árak függvényében.

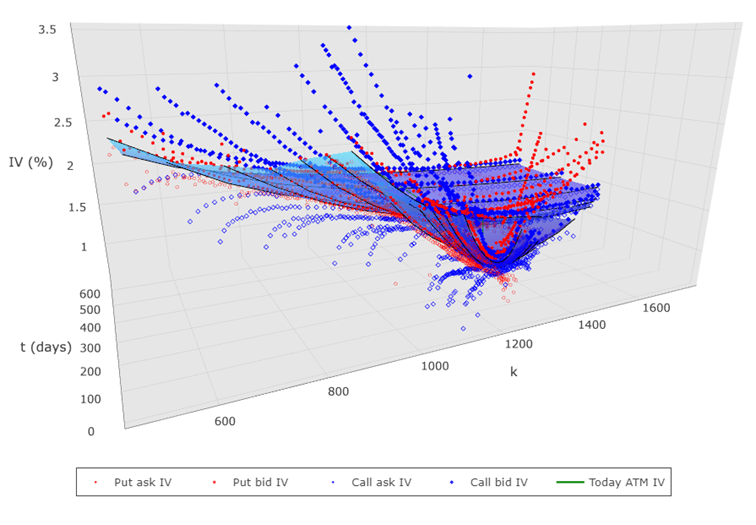
Forrás: Interactive Brokers

A képen jól látszik, hogy az aktuális részvényártól strike-onként (k) távolodva hogyan nő a beárazott volatilitás (IV%) (ezt a jelenséget hívják volatilitás mosolynak), valamint másik érdekesség, hogy a távoli opciók bid/ask spread-je mennyire kitágul (a legnagyobb likviditás az at-the-money opcióknál jellemző).

Görögök

A modelből következnek bizonyos paraméterek, amik megadják, hogy az opció értéke ceteris paribus milyen körülmény megváltozására mennyire érzékeny. Ezeket a paramétereket opciós görögöknek nevezzük, noha nem mind valódi görög betű, különösen az ennél magasabb rendű deriváltak.

• Delta: Megadja, hogy az alaptermék árának elmozdulása milyen mértékben hat az opció árára. Jellemzően egy -1 és 1 közötti szám, ahol az előjel megmutatja a hatás irányát (pl.: long put, vagy short call opciónál negatív). A változás mértéke abszolútértékben, annál inkább tolódik a 0 felé, minél inkább out of the money egy opció, és fordítva. Az egyre nagyobb implicit volatilitás „kiszélesíti” a deltákat az opciós strike-ok függvényében, hiszen a nagyobb bizonytalanság több lehetséges kötési árat fed le. Sokan az opció beválási valószínűségével (moneyness) teszik egyenlővé. Ez a megfogalmazás nem túl pontos, de valóban használható az analógia: a piac nagyjából delta valószínűséggel árazza, hogy az opció in the money jár majd le.
• Gamma: Második derivált, a delta változását mutatja meg az alaptermék változásának függvényében – kvázi a delta „gyorsulása”. A delta hedgeléskor komoly jelentősége van, mivel egy pozíció gamma fedezését követően a delta érzékenységét kvázi elimináljuk, így a fedezés jóval érzéketlenebb lesz az alaptermék árelmozdulására.
• Vega: Az opció árának érzékenységét mutatja meg a volatilitás megváltozására.
• Theta: Az opció időérzékenységét mutatja meg, azaz leegyszerűsítve, hogy mennyit veszít értékéből az opció az idő előre haladása miatt csökkenő bizonytalanság által (time decay). Főleg az out of the money opcióknál jelentős, hiszen azoknál nem beszélhetünk belső értékről. A lejárathoz egyre közeledve az értékvesztés gyorsul.
• Rho: Az opció árának érzékenysége a kockázatmentes kamatláb változására. Jellemzően csak nagyon hosszú opcióknál, és magas kamatkörnyezetben van érdemi jelentősége.

Fentieken túl még vannak jóval egzotikusabb görögök, melyek jellemzően magasabb rendű deriváltak, de ezekkel már csak azoknak van dolga, akik matematikai modelleket építenek a Black–Scholes-modell hátán. Az egyes érzékenységi paraméterek mind egymás függvényében is változnak. Ebből az átlag opciókereskedő számára jellemzően a volatilitás és az idő változása az, amivel leginkább számolni kell.

A bejegyzésben foglaltak kizárólag az író személyes véleményét tükrözik és nem tekinthetőek az Erste Bank Hungary Zrt., az Erste Befektetési Zrt. vagy az Erste Alapkezelő Zrt. hivatalos szakmai álláspontjának. A bejegyzés tartalma nem minősül befektetési ajánlatnak, ajánlattételi felhívásnak, befektetési tanácsadásnak vagy adótanácsadásnak.

Címlapkép: Shutterstock