A tömeg, a tér és az idő
Talán sokan ismerik azt a viccet, hogy:
- Mi az összefüggés a tér, az idő meg a tömeg között?
- ?
- Hát, ha jó az idő, akkor nagy tömeg van a téren!
Szakállas boomer vicc, s most nem is erről fogok írni, hanem az autózás és az autók tömegének kapcsolatáról.
Sokszor hallom mostanában az elektromos autókkal kapcsolatban, hogy micsoda pocséklás azt a nagy tömeget mozgatni. Ugyanis az akkumulátor nagy tömege miatt az elektromos autók súlya általában jelentősen meghaladja a hagyományos belső égésű motorral szerelt gépkocsik súlyát. Pedig ez nem így van. Ugyanis — mint tudjuk — az elektromos autók fékezéskor a mozgási energiát — amely ~1/2*m*v2 — visszaalakítják elektromos energiává, míg pl. a benzines gépkocsik — a más hajtáslánc miatt — erre nem képesek, illetve nincs sok értelme ilyen eszközt beépíteni. Vagyis, ha egy nagytömegű benzin üzemű gépkocsit használunk a városban, akkor a folyamatos megállások és gyorsítások annak ellenére is számottevő energiát visznek el, hogy az igazán fájó tényező — a sebesség négyzet — kis sebességeknél még relatíve pici. Viszont az „m” tömeggel arányos energiafelhasználásról beszélünk. Vagyis számít a tömeg. Ugyanakkor egy elektromos autónál minél közelebb van a visszatöltés a 100 százalékhoz, annál kevésbé számít a tömeg. Ideális esetben szinte semennyire, legalábbis a mozgási energia szempontjából. A gördülési ellenállásnál viszont számít a tömeg, s abban az elektromos autó rosszabb, de az együttes energiamérleg általában még mindig inkább az elektromos autó oldalára billenti a mérleget. Ugyanis egy elektromos gépkocsi tipikusan két liter benzin egyenértékes energiából elautózik a városban. Persze ebben a hatékonyság is komoly szerepet játszik, ami egy belső égésű motor esetében alacsony, 30-40 százalék között van. A Toyota Prius gépkocsija éppen ezért volt olyan népszerű, mert akkor, amikor a benzines gépkocsik még 8-10 litert fogyasztottak városban, a Prius a mozgási energia visszanyerésével ezt lecsökkentette 5-6 liter környékére, a kettős benzines és elektromos motor alkalmazásával.
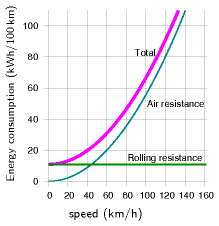
Ha nagy sebességgel haladunk, akkor viszont az erő — amelyet le kell küzdenünk — leginkább a közegellenállásból adódik. Annak a legfájóbb komponense a sebesség négyzetes tagja. Ez így néz ki: F=1/2*ρ*Cd*A*v2, ahol F az erő (ellentétes a mozgásiránnyal), ρ a közeg sűrűsége (levegő 1,2 kg/m3), A az effektív felület (egy átlagos kocsinál tipikusan 0,74m2), a Cd pedig a közegellenállási együttható. Az utóbbi egy jó kocsinál 0,2, egy rosszabb közegellenállásúnál pedig 0,3, vagy a fölötti érték. Mint láthatjuk, ebben a kifejezésben sehol sem szerepel a tömeg.
S hogy mennyivel nagyobb erőt kell leküzdenünk, azaz mennyivel több energiát használunk, ha pl. kétszeres sebességgel haladunk? A gördülési ellenállás és egyéb ellenállások fölött ez négyszeresre növekszik.
A fogyasztás és a sebesség kapcsolata